https://www.acmicpc.net/problem/1965

백준 상자 넣기 문제를 풀기 위해서는 DP(동적 계획법)을 활용하면 된다.
🌘 문제 이해하기
- 정육면체 모양의 상자가 일렬로 늘어서 있다.
- 상자마다 크기가 주어져 있는데, 앞에 있는 상자의 크기가 뒤에 있는 상자의 크기보다 작으면, 앞에 있는 상자를 뒤에 있는 상자 안에 넣을 수가 있다.
- 예를 들어 크기 1인 상자를 크기 5인 상자에 넣고, 다시 이 상자를 크기 7인 상자 안에 넣을 수 있다.
- 상자의 크기가 주어질 때, 한 번에 넣을 수 있는 최대의 상자 개수를 출력하는 프로그램을 작성하시오.
- 첫째 줄에 한 줄에 넣을 수 있는 최대의 상자 개수를 출력한다.
🌗 문제 자세히보기
동적 계획법 문제는 기준점을 정하고 그 이전의 값들과 비교를 하는 것이다.
한 줄에 넣을 수 있는 최대의 상자 개수를 구하는 것이므로 비교 값이 기준 값보다 작으면 +1 로 늘려주면 된다.
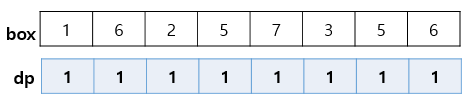
위에 있는 배열은 상자의 한변을 저장한 box 배열
아래 있는 배열은 담을 수 있는 상자들의 수를 저장한 dp배열 이다.
이제 기준값을 정하고 그 이전의 값들과 비교하면 된다.
첫번째 박스는 비교 대상이 없으니 1로 고정
1. 두번째 박스
- 첫번째 박스와 길이를 비교

box[1] > box[0]
dp[1] = Math.max(dp[1], dp[0]+1) = Math.max(1,2) = 2
2. 세번째 박스
- 첫번째 박스와 길이 비교

box[2] > box[0]
dp[2] = Math.max(dp[2], dp[0]+1) = Math.max(1,2) = 2
- 두번째 박스와 길이 비교

box[2] < box[1]
두번째 박스는 더 커서 상자안에 넣을 수 없다.
3. 네번째 박스
- 첫번재 박스와 길이 비교

box[3] > box[0]
dp[3] = Math.max(dp[3], dp[0]+1) = Math.max(1,2) = 2
- 두번째 박스와 길이 비교

box[3] < box[1]
두번째 박스는 더 커서 상자안에 넣을 수 없다.
- 세번째 박스와 길이 비교

box[3] < box[2]
dp[3] = Math.max(dp[3], dp[2]+1) = Math.max(1,3) = 3
4. 다섯번째 박스

위와 같은 방식으로 모든 수의 증가하는 부분 수열을 구하고 그 중 최대길이를 출력한다.
🌕 최종코드
import java.io.*;
import java.util.StringTokenizer;
public class Main{
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine()); //상자의 개수
long[] box = new long[n+1];
int[] dp = new int[n+1];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0;i<n;i++)
{
box[i]= Integer.parseInt(st.nextToken()); //상자 길이 넣기
dp[i] = 1;
}
int asnwer = 0;
for(int i=0;i<n;i++) //기준값
{
for(int j=0;j<i;j++) //비교값
{
if(box[i]>box[j]) //기준값 보다 비교값이 더 작을 때
{
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
asnwer = Math.max(asnwer,dp[i]);
}
System.out.println(asnwer);
}
}'항해' 카테고리의 다른 글
| [Day32]JAVA 백준 가장 긴 바이토닉 부분 수열(11054번) (0) | 2024.11.28 |
|---|---|
| [Day31]JAVA 백준 줄세우기(2631번) (0) | 2024.11.27 |
| [Day29]JAVA 백준 파도 수열(9461번) (0) | 2024.11.25 |
| [Day28]JAVA 백준 가장 큰 증가하는 부분 수열(11055번) (0) | 2024.11.24 |
| [Day27]JAVA 백준 가장 긴 감소하는 부분 수열(11722번) (0) | 2024.11.23 |



