https://www.acmicpc.net/problem/11663

🌘 문제 이해하기
- 일차원 좌표상의 점 N개와 선분 M개가 주어진다.
- 첫째 줄에 점의 개수 N과 선분의 개수 M이 주어진다. (1 ≤ N, M ≤ 100,000)
- 둘째 줄에는 점의 좌표가 주어진다.
- 셋째 줄부터 M개의 줄에는 선분의 시작점과 끝점이 주어진다.
- 입력으로 주어진 각각의 선분 마다, 선분 위에 입력으로 주어진 점이 몇 개 있는지 출력한다.
🌗 문제 자세히보기
- 선분 위에 주어진 점이 몇개 있는 지 구하기 위해서는 일차원 좌표상에 일치하는 선분의 좌표 범위를 구하면 되는 것이다.
아래 그림과 같이 시작점이 5 끝점이 25 인 선분에 있는 선분이 점 3 과 30 사이에 위치하는 것을 파악하고 이의 범위를 구하는 것이다.

시작점 5 가 점3 과 점10 사이에 위치하는 것을 파악하기 위해 이탐색으로 적절한 범위를 찾는 것이다.
🚩 시작점의 범위 , 끝점의 범위 를 각각 구하는 것이 포인트다.
선분 5 - 25 를 예시를 범위를 구하는 방법을 풀어보겠다.
(편의를 위하여 점의 좌표를 배열에 담고 인덱스는 1부터 시작한다. )
//점의 좌표
int [] nArr = new int[n+1];
st = new StringTokenizer(br.readLine());
for(int i=1;i<=n;i++)
{
nArr[i] = Integer.parseInt(st.nextToken());
}
1. 시작점 의 범위를 이탐색을 활용하여 구한다.
int startLeft = 1;
int startRight = n;
int endLeft = 1;
int endRight = n;
int startPoint = mArr[i][0];
int endPoint = mArr[i][1];
int startMid = 0;
int endMid = 0;
//최종 시작,끝 범위
int start =0, end=0;
while(startLeft <=startRight)
{
startMid = (startLeft+startRight)/2;
//선분 시작점이 범위보다 작으면 범위를 더 낮은 쪽으로 이동
if(startPoint < nArr[startMid])
{
start = startMid;
startRight = startMid-1;
}
else if( startPoint == nArr[startMid])
{
//선분 시작점과 점의 좌표가 동일한 경우
start = startMid;
break;
}
else
{
//선분 시작점이 범위보다 크면 범위를 더 큰 쪽으로 이동
startLeft = startMid+1;
}
}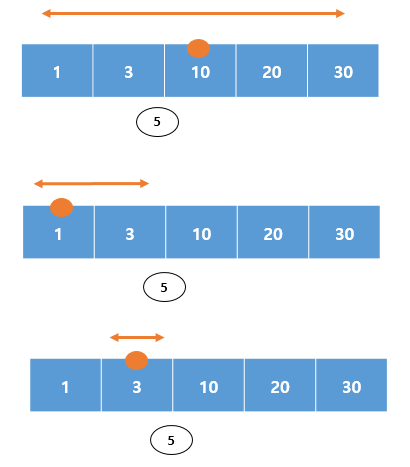
1. startMid = (1 + 5)/2 = 3 으로 nArr[3] = 10 이 된다.
2. 5는 10보다 작으므로 범위를 더 작은 쪽으로 이동한다.
startRight = startMid -1 = 3-1 = 2
3. startMid = (1+2)/2 = 1 으로 nArr[1] = 1 이 된다.
4. 5는 1보다 크기때문에 범위를 더 큰 쪽으로 이동한다.
startLeft = startMid +1 = 1+ 1 = 2
5. startMid = (2+2)/2 = 2 으로 nArr[2] = 3 이 된다.
6. 5는 3보다 크기때문에 범위를 이동해야 하지만 이때 while 문 조건에 맞지않아 벗어난다.
이에 간선의 시작점5는 점10 밑에 존재하는 것을 알 수 있다.
다르게 말하자면 점3은 간선의 범위에 포함되지 않고 10은 간선의 범위에 포함이 되는 것이다.
그래서 시작범위를 인덱스 3 (nArr[3] = 10) 으로 저장되는 것이다.
2. 끝점 의 범위를 이탐색을 활용하여 구한다.
//끝점
while(endLeft <= endRight)
{
endMid = (endLeft+endRight)/2;
//선분 끝점이 범위보다 크면 범위를 더 큰쪽으로 이동
if(endPoint > nArr[endMid])
{
end =endMid;
endLeft = endMid+1;
}
else if(endPoint == nArr[endMid])
{
//선분 끝점과 점의 좌표가 동일한 경우
end =endMid;
break;
}
else
{
//선분 끝점이 범위보다 작으면 범위를 더 작은 쪽으로 이동
endRight = endMid-1;
}
}
1. endMid = (1 + 5)/2 = 3 으로 nArr[3] = 10 이 된다.
2. 25는 10보다 크기때문에 범위를 더 큰 쪽으로 이동한다.
endLeft = endMid+1 = 3 + 1 = 4
3. endMid = (4+5)/2 = 4 으로 nArr[4] = 20 이 된다.
4. 25는 20보다 크기때문에 범위를 더 큰 쪽으로 이동한다.
endLeft = endMid+1 = 4 + 1 = 5
5. startMid = (5+5)/2 = 5 으로 nArr[5] = 30 이 된다.
6. 25는 30보다 작기 때문에 범위를 이동해야 하지만 이때 while 문 조건에 맞지않아 벗어난다.
이에 간선의 끝점이 점30 밑에 존재하는걸 알 수 있다.
즉 점20은 간선에 포함되고 점30은 간선에 포함되지 않는다.
그래서 끝 범위가 인덱스 4 (nArr[4] = 20) 으로 저장되는 것이다.

3. 시작범위와 끝범위 사이의 포함된 총 점의 개수 구하기
간선에 포함되는 첫번째 점의 좌표와 마지막 점의 좌표를 구하여 그 사이의 존재하는 점의 개수를 구하면 되는 것이다.
시작범위 인덱스를 3 , 끝범위 인덱스가 4 이면 총 점의 개수 : 4 - 3 + 1 = 2
총 점의 개수 : 끝범위 인덱스 - 시작범위 인덱스 + 1
그리고 시간을 단축하기 위해서 미리 예외처리를 해주면 좋은 경우들이 있다.
1. 간선의 범위가 점의 전체 좌표 범위보다 크거나 작을때는 간선에 포함된 점이 없으므로 바로 0 출력
ex)

이탐색을 두번해야 한다는 것이 헷갈릴수 있는데 차근차근 직접 범위를 지정하고 이진탐색으로 중간값을 구해보면 이해가 될 것이다.
🌕 최종코드
import java.io.*;
import java.util.*;
public class Main{
public static void main(String[] args) throws IOException
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st= new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
//점의 개수
int n = Integer.parseInt(st.nextToken());
//선분의 개수
int m = Integer.parseInt(st.nextToken());
//점의 좌표
int [] nArr = new int[n+1];
st = new StringTokenizer(br.readLine());
for(int i=1;i<=n;i++)
{
nArr[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(nArr); //오름차순 정렬
int[][] mArr = new int[m][2];
//선분의 시작점 끝점 저장
for(int i=0;i<m;i++)
{
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
mArr[i][0] = u;
mArr[i][1] = v;
}
for(int i=0;i<m;i++)
{
int startLeft = 1;
int startRight = n;
int endLeft = 1;
int endRight = n;
int startPoint = mArr[i][0];
int endPoint = mArr[i][1];
int startMid = 0;
int endMid = 0;
int start =0, end=0;
if(startPoint > nArr[n])
{
//1. 선분이 점의 좌표 범위보다 위에 있는 경우
sb.append("0\n");
}
else if(endPoint < nArr[1])
{
//2. 선분이 점의 좌표 범위보다 아래에 있는 경우
sb.append("0\n");
}
else
{
//첫 시작점이 처음 점의 좌표보다 작거나 같을때는 무조건 처음 점이 포함된다.
if(startPoint <= nArr[1])
{
start = 1;
}
else
{
//시작점
while(startLeft <=startRight)
{
startMid = (startLeft+startRight)/2;
//선분 시작점이 범위보다 작으면 범위를 더 낮은 쪽으로 이동
if(startPoint < nArr[startMid])
{
start = startMid;
startRight = startMid-1;
}
else if( startPoint == nArr[startMid])
{
//선분 시작점과 점의 좌표가 동일한 경우
start = startMid;
break;
}
else
{
//선분 시작점이 범위보다 크면 범위를 더 큰 쪽으로 이동
startLeft = startMid+1;
}
}
}
//끝점이 마지막 점의 좌표보다 작거나 같을때는 무조건 마지막 점이 포함된다.
if(endPoint >= nArr[n])
{
end = n;
}
else
{
//끝점
while(endLeft <= endRight)
{
endMid = (endLeft+endRight)/2;
//선분 끝점이 범위보다 크면 범위를 더 큰쪽으로 이동
if(endPoint > nArr[endMid])
{
end =endMid;
endLeft = endMid+1;
}
else if(endPoint == nArr[endMid])
{
//선분 끝점과 점의 좌표가 동일한 경우
end =endMid;
break;
}
else
{
//선분 끝점이 범위보다 작으면 범위를 더 작은 쪽으로 이동
endRight = endMid-1;
}
}
}
int result = end - start +1;
sb.append(result+"\n");
}
}
System.out.println(sb);
}
}'항해' 카테고리의 다른 글
| [DAY41] 99클럽 코딩테스트 JAVA 백준 두 용색 2470번 (0) | 2025.01.17 |
|---|---|
| [DAY40] 99클럽 코딩테스트 JAVA 백준 기타 레슨 2343번 (0) | 2025.01.16 |
| [DAY38] 99클럽 코딩테스트 JAVA 백준 랜선자르기 1654번 (0) | 2025.01.14 |
| [DAY37] 99클럽 코딩테스트 JAVA 백준 암기왕 2776번 (시간초과 해결) (0) | 2025.01.13 |
| [DAY37] JAVA프로그래머스 전화번호 목록 (0) | 2024.12.17 |



